【Ray Tracing】光线追踪——光线的定义

type

Post

status

Published

date

Nov 24, 2022

slug

raytracing_ray

summary

光线是实现光线追踪的基础，本章将说明如何实现一条光线。光线的一些性质在实现一条光线之前，首先应该要定义光的一些性质（不考虑波动性），假设光线具有以下几个性质（并不是现实中的物理性质）： 1. 光线沿着直线传播 2. 光线之间无法碰撞 3. 光线从光源开始传播到眼睛中（中途可发生反射和折射） 4. 光线路径可逆，即从A发出的到B的光线，一定也可以从B发出到A

光线的一些性质

在实现一条光线之前，首先应该要定义光的一些性质（不考虑波动性），假设光线具有以下几个性质（并不是现实中的物理性质）：

光线沿着直线传播

光线之间无法碰撞

光线从光源开始传播到眼睛中（中途可发生反射和折射）

光线路径可逆，即从A发出的到B的光线，一定也可以从B发出到A

其中，第4条性质是作为光线追踪实现的重要性质，因为实现时我们选择让光线从眼睛出发逆着光路传播，一直到光源结束。

光线的定义

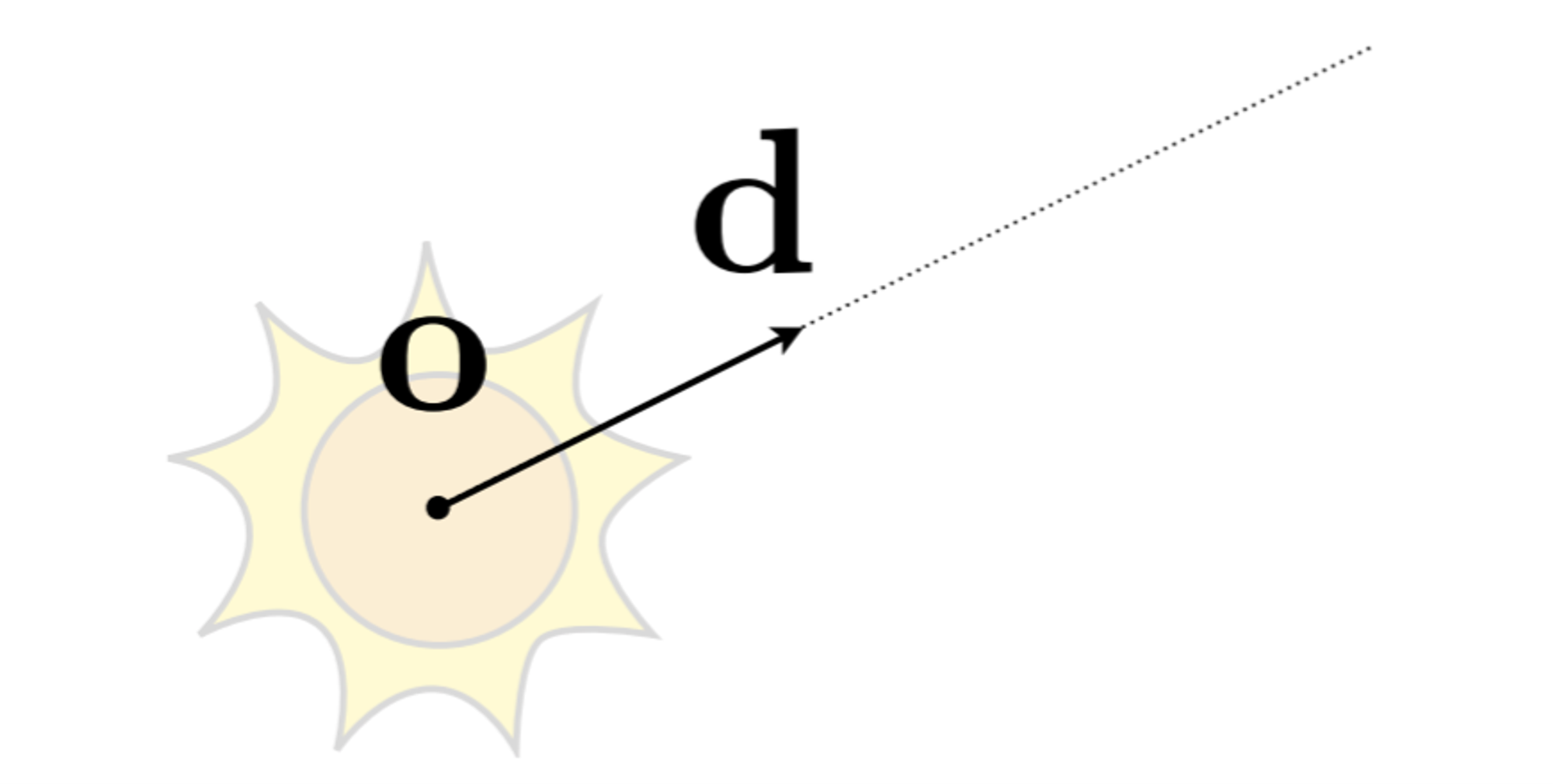
光线指的是由光源出发，到任意方向的一条光路。在数学上，光线可以用一条射线表示，对于一条射线，通常可以定义为一个起点\$o\$和一个方向向量\$\boldsymbol{d}\$组成：

$$ \boldsymbol{r}(t) = \boldsymbol{o} + t\boldsymbol{d}, 0 < t < \infty $$

其中，\$t\$为时间，表示光线从光源出发经过的时间，注意这里光线并不具有物理上的光的传播速度光速，同时，可以设置一个\$t_{max}\$表示光线可以传播的最大时间，这样光线的传播距离就被限制为了\$[0,r(t_{max})]\$。

光线与物体的交点

当光线和物体相遇，光线会与物体相交于一点，我们需要求出此时的\$t\$值，从而得到交点坐标。

光线和球面的交点

对于隐式几何，我们可以很容易求出几何图形与光线的交点，以球面为例我们来看一下具体的计算过程。

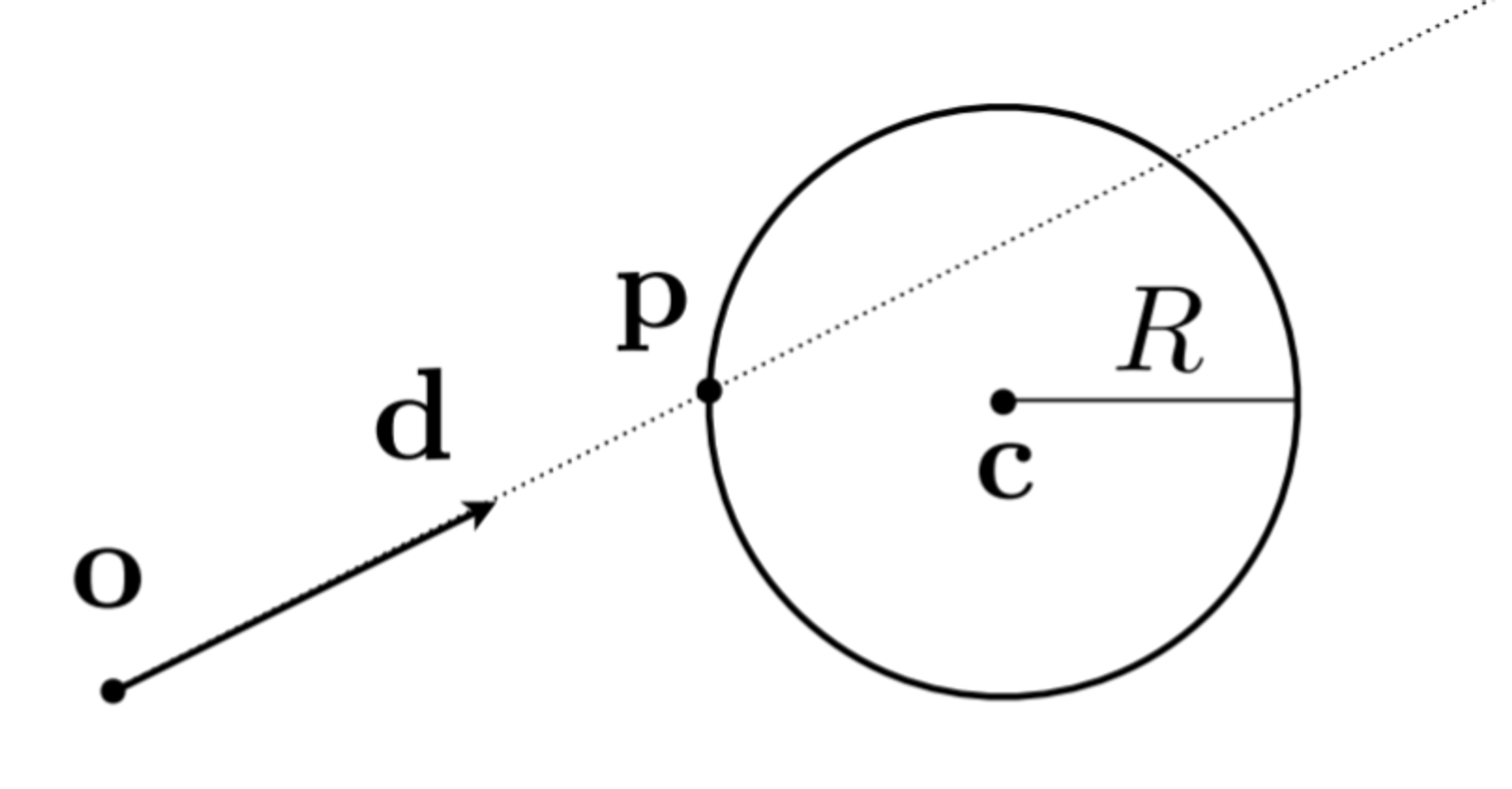
假设：

光线\$\boldsymbol{r}(t) = \boldsymbol{o}+t\boldsymbol{d}\$

球面\$P: (\boldsymbol{P} - \boldsymbol{C})^2 - R^2 = 0\$

求交点，就可以把光线方程带入球面方程解一元二次方程，得到\$t\$，即 $$ (\boldsymbol{o}+t\boldsymbol{d} - \boldsymbol{C})^2-R^2 = 0 $$

通过整理为\$at^2+bt+c=0\$的形式，可得到\$a=\boldsymbol{d} \cdot \boldsymbol{d}\$，\$b=2(\boldsymbol{o}-\boldsymbol{C})\cdot \boldsymbol{d}\$，\$c=(\boldsymbol{o}-\boldsymbol{C})(\boldsymbol{o}-\boldsymbol{C}) - R^2\$。

最后通过求根公式\$t=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\$，即可求解。

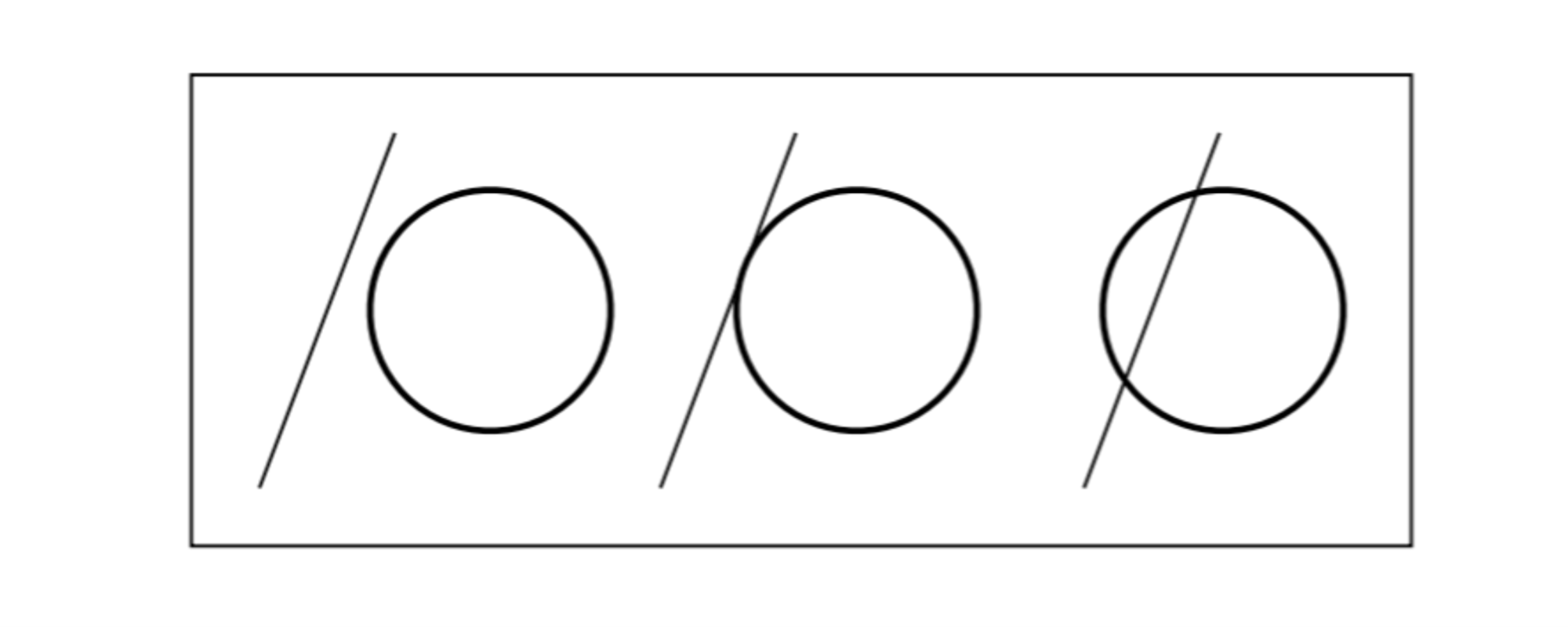
当然，这里求出来有三种情况，一种情况\$b^2-4ac<0\$此时该方程无实数根，即光线与球面并不相交；第二种\$b^2-4ac=0\$此时有一个根，光线与球面相切，切点即为交点；第三种\$b^2-4ac>0\$存在两个根，我们只需要保留较小的那一个，因为远处的交点光线并不会照到。

注意：\$0<t<\infty\$这个条件一定要验证。

光线与三角面的交点

但是对于显示几何（使用多边形面构造的几何），计算交点就不那么容易了，下面以三角形面为例来看一下如何求与光线的交点。

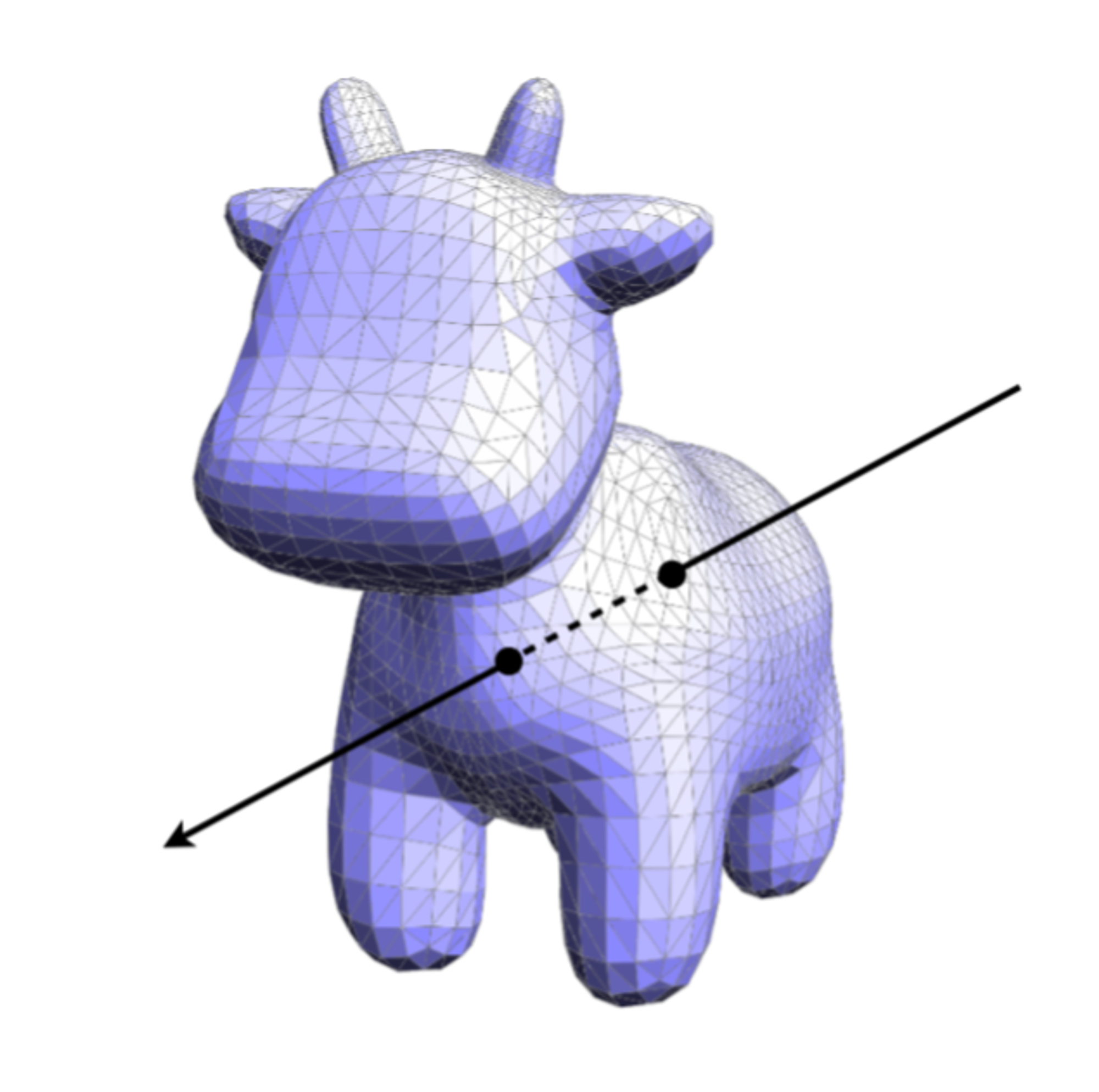
基本思路是：先测试以下光线与三角形所在平面是否有交点，然后再验证与平面的交点是否在三角形内。

我们假设一直这个平面的法线\$\boldsymbol{N}\$，以及在平面上的一个点\$\boldsymbol{P'}\$，那么，这个平面的方程就可以写为\$(\boldsymbol{P}-\boldsymbol{P'})\cdot \boldsymbol{N} = 0\$。

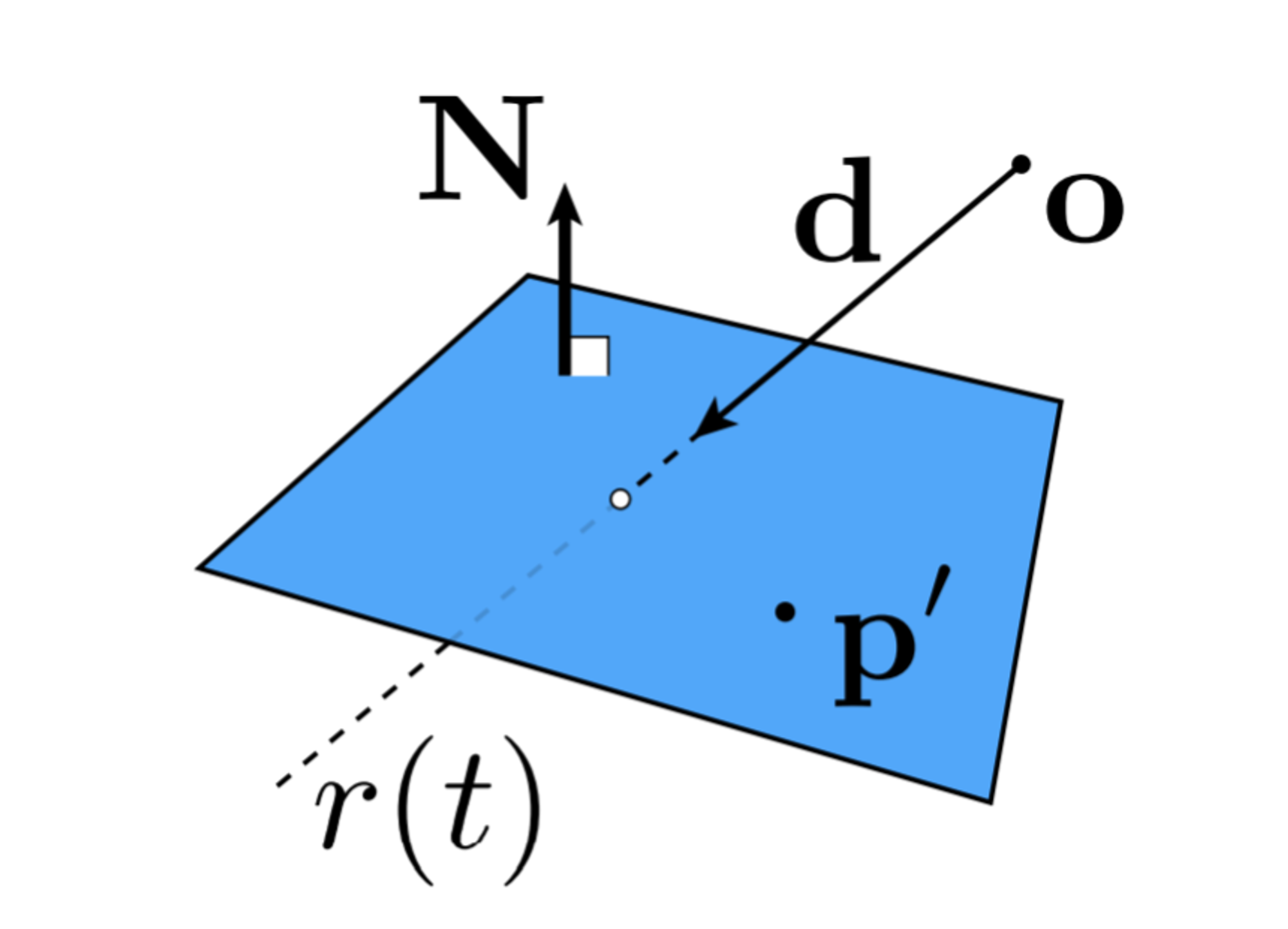
按照上面的方法，我们将光线方程代入平面的方程，即\$(o+t\boldsymbol{d})\cdot\boldsymbol{N}=0\$，可以解得 $$ t = \frac{(\boldsymbol{p'}-\boldsymbol{o})\cdot \boldsymbol{N}}{\boldsymbol{d}\cdot\boldsymbol{N}} $$

同样，需要验证\$0<t<\infty\$。

接下来，就可以验证交点是否在三角形内了，方法就有很多了，可以用向量的点积计算，也可以用向量的叉积计算，这里不赘述了。

在这里，单独介绍一个Möller-Trumbore算法来方便计算光线与三角面的交点坐标。

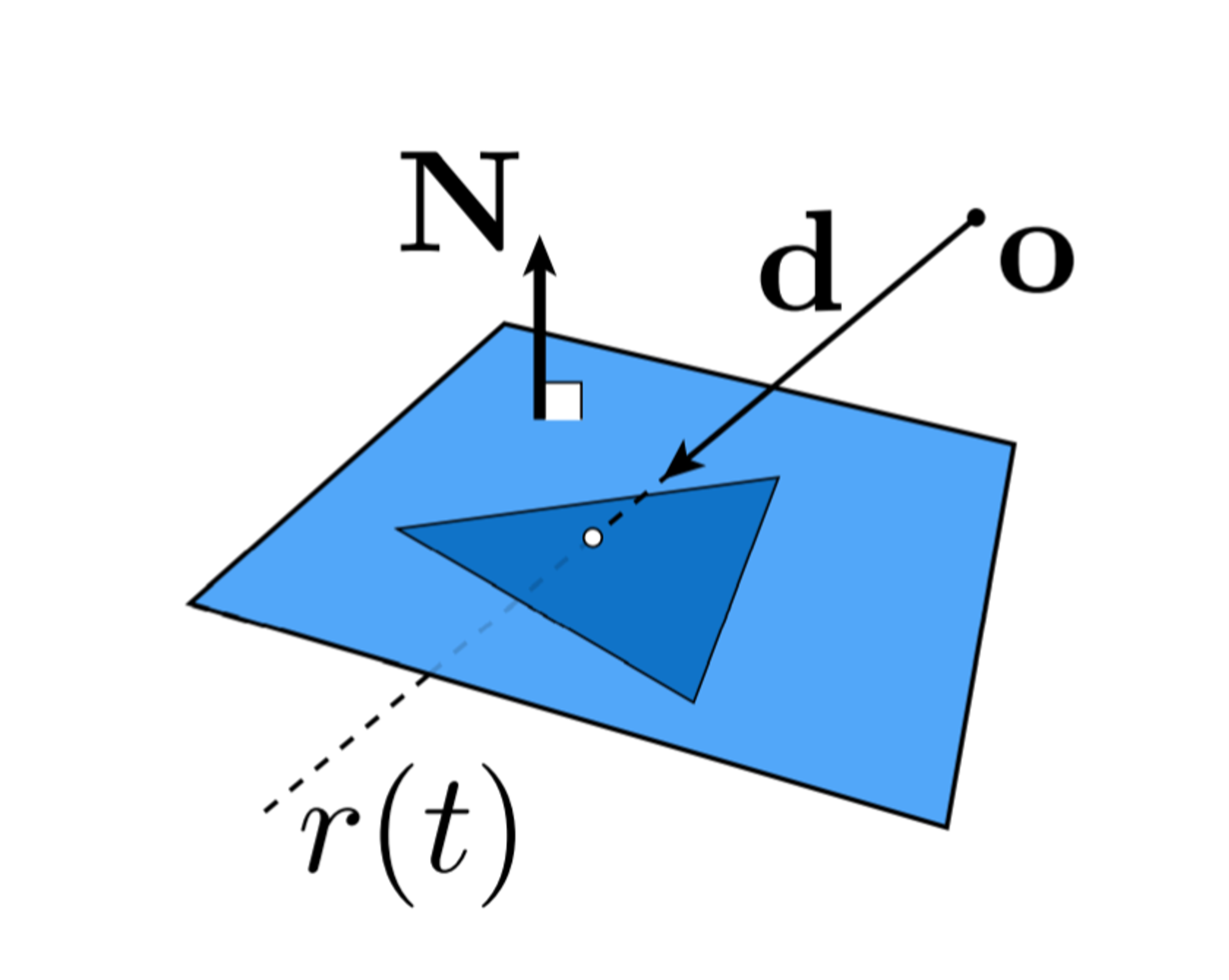
根据几何关系，我们很容易知道，光线相交于三角面内部的点可以表示成下面这种形式： $$ \boldsymbol{O}+t\boldsymbol{D}=(1-b_1-b_2)\boldsymbol{P_0}+b_1\boldsymbol{P_1}+b2\boldsymbol{P_2} $$ 接下来就只需要计算下面这个式子，就可以解出上式中的\$t\$，\$b_1\$，\$b_2\$，当然，我们只需要\$t\$就可以了。 $$ \begin{bmatrix} t\\\\ b_1\\\\ b_2 \end{bmatrix} = \frac{1}{\boldsymbol{S_1}\cdot\boldsymbol{E_1}}\begin{bmatrix} \boldsymbol{S_2}\cdot\boldsymbol{E_2}\\\\ \boldsymbol{S_1}\cdot\boldsymbol{S}\\\\ \boldsymbol{S_2}\cdot\boldsymbol{D} \end{bmatrix} $$ 其中，\$\boldsymbol{E_1}=\boldsymbol{P_1}-\boldsymbol{P_0}\$，\$\boldsymbol{E_2}=\boldsymbol{P_2}-\boldsymbol{P_0}\$，\$\boldsymbol{S}=\boldsymbol{O}-\boldsymbol{P_0}\$，\$\boldsymbol{S_1}=\boldsymbol{D}\times\boldsymbol{E_2}\$，\$\boldsymbol{S_2}=\boldsymbol{S}\times\boldsymbol{E_1}\$。

关于Möller-Trumbore算法的推导，将会放在另一篇文章中，目前可以直接使用就可以了。

光线的投射

上面我们讨论了如何定义一条光线以及光线与物体相交的算法，现在我们需要把光线投射出去，方法很简单，对每个像素点，都由眼睛位置发射一条光线这样光线方向就可以确定了。

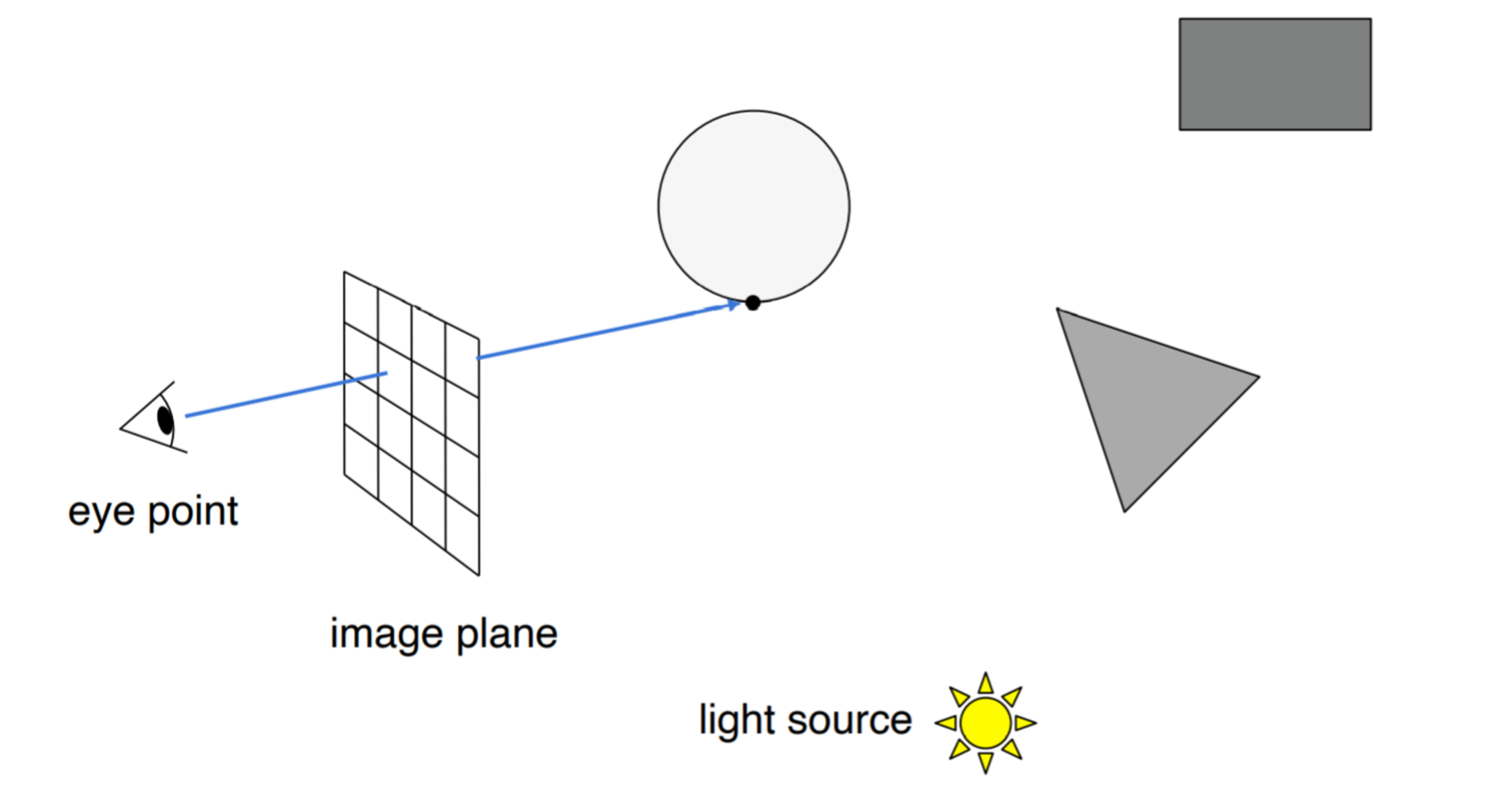
下面给出一些定义：

视野（field-of-view，fov），这里表示可视角度，通常只使用纵向的视野，表示为fovY，配合纵横比来使用。

纵横比（aspect radio），画面长度与宽度的比值。

有了上面的定义，下面我们来具体计算一下光线的投射方向的计算:

首先，需要将每个像素点的坐标映射到\$[-1,1]\$之间

$$ x_s = (\frac{2x}{w}-1)\times s \times \alpha\\\\ y_s = (1-\frac{2y}{h})\times s \\\\ z_s = -1 $$

其中，\$s = \tan \frac{fovY}{2}\$，\$\alpha\$为纵横比，得到的坐标就是映射后的像素坐标\$(x_s,y_s,z_s)\$，可以看做方向向量，下面就要将得到的方向向量进行归一化，得到相应方向的单位向量\$(x',y',z')\$。

$$ x' = \frac{x_s}{\sqrt{x_s^2+y_s^2+z_s^2}}\\\\ y' = \frac{y_s}{\sqrt{x_s^2+y_s^2+z_s^2}}\\\\ z' = \frac{z_s}{\sqrt{x_s^2+y_s^2+z_s^2}} $$

之后就可以将光线投射出去，写成伪代码：


Render()
  for each pixel with (x,y)
    color(pixel) = Trace(ray_through_pixel(x,y))

总结

本章介绍了如何构造一条光线，并将光线投射出去求出与物体的交点，这样就基本实现了一个最简单的光线追踪框架，在下一章我们将会继续探究光线追踪。

参考文献

[1] Real-Time Rendering 4th Edition. Tomas Akenine-Moller, Eric Haines, Naty Hoffman, Angelo Pesce, et al.

[2] Physically Based Rendering 3rd Edition. Matt Pharr, Wenzel Jakob, Greg Humphreys.

[3] GAMES101. Lingqi Yan(闫令琪).

[4] 计算机图形学十二：Whitted-Style光线追踪原理详解及实现细节. 孙小磊. https://zhuanlan.zhihu.com/p/144403005