type
Post
status
Published
date
Nov 24, 2022
slug
decision_tree
summary
决策树是一种基本的分类和回归算法。
决策树模型呈树形结构,可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
决策树模型由结点和有向边组成,结点分为内部结点和叶结点,内部结点表示特征,叶结点表示类,有向边表示某一特征的取值。
tags
机器学习
Python
人工智能
数据分析
category
机器学习
icon
password
Property
Nov 24, 2022 01:39 PM
决策树是一种基本的分类和回归算法。
决策树模型呈树形结构,可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
决策树模型由结点和有向边组成,结点分为内部结点和叶结点,内部结点表示特征,叶结点表示类,有向边表示某一特征的取值。
决策树模型与学习
决策树模型
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:内结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或者属性,叶结点表示一个类。
决策树与if-then规则
可以将决策树看成是一个if-then规则的集合。将决策树转化成if-then规则的过程是这样的:由决策树的根结点到叶结点的每一条路径构建一条规则;路径上内部结点的特征对应着规则的条件,而叶结点的类对应着规则的结论。
决策树与条件概率分布
决策树还表示给定特征条件下的类的条件概率分布。这一条件概率分布定义在特征空间的一个划分(partition)上。将特征空间划分为互不相交的单元(cell)或者区域(region),并在每个单元定义一个类的概率分布就构成了一个条件概率分布。
决策树学习
决策树学习,假定给定训练数据集
$$D = \{ (x_1,y_1),(x_2,y_2),...,(x_n,y_n) \}$$,
其中\\(x_i = (x_i^{(1)},x_i^{(2)},...,x_i^{(n)} )^T\\),\\(n\\)为特征个数,\\(y_i\in \{ 1,2,...,K \}\\),为类的标记,\\(i=1,2,...,N\\),\\(N\\)为样本容量。学习的目标是根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确的分类。
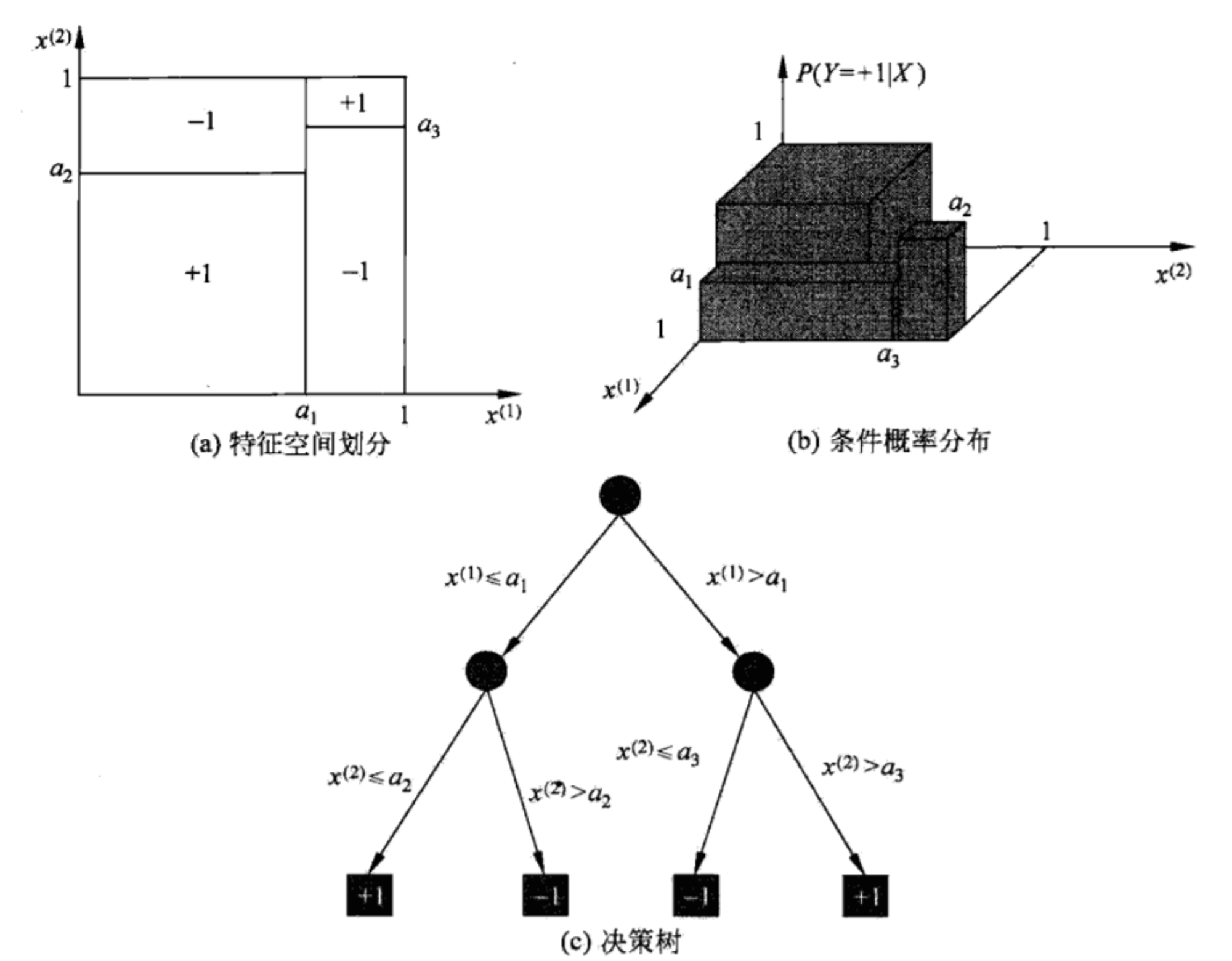
决策树学习本质上是从训练数据集中归纳出一组分类规则。我们需要的是一个与训练数据矛盾较小的决策树,同时具有很好的泛化能力。另一个角度看,决策树学习是由训练数据集估计条件概率模型。我们选择的条件概率模型应该不仅对训练数据有很好的拟合,而且对未知数据有很好的预测。
决策树学习用损失函数表示这一目标。如下所述,决策树学习的损失函数通常是正则化的极大似然函数。决策树学习的策略是以损失函数为目标函数的最小化。
当损失函数确定以后,学习问题就变为在损失函数意义下选择最优决策树的问题。因为从所有可能的决策树中选取最优决策树是NP完全问题(NP的英文全称是Non-deterministic Polynomial的问题,即多项式复杂程度的非确定性问题),所以现实中决策树学习算法通常采用启发式方法,近似求解这一最优化问题。这样得到的决策树是次最优(sub-optimal)的。
决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得对各个子数据集有一个最好的分类的过程。
学习模型:根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确分类。该模型不仅对训练数据有很好的拟合,而且对未知数据有很好的越策
学习策略:通常选择正则化的极大似然函数作为损失函数,损失函数最小化
学习算法:采用启发式算法,近似求解上述最优化问题。递归地选择最优特征,并根据该特征对训练数据进行分割,使得对各个子数据集有一个最好的分类。
过拟合:以上方法生成的决策树可能对训练数据有很好的分类能力,但对未知的数据却未必,即可能发生过拟合。
剪枝:对生成的树自下而上进行剪枝,将树变得更简单,从而使它具有更好的泛化能力。
特征选择:如果特征数量很多,也可以在学习开始的时候,对特征进行选择。
特征选择
特征选择问题
特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。通常特征选择的准则是信息增益或信息增益比。
信息增益
熵
在信息论与概率统计中,熵(entropy)是表示随机变量不确定性的度量。设\\(X\\)是一个取有限个值的离散随机变量,其概率分布为
$$P(X=x_i)=p_i, i=1,2,...,n$$
则随机变量\\(X\\)的熵定义为
$$H(X)=-\sum \limits_{i=1}^n p_i \log p_i$$
通常上式中的对数以2为底或者以自然对数e为底,这时熵的单位分别称作比特(bit)或纳特(nat)。由定义可知,熵只依赖于\\(X\\)分布,而与\\(X\\)的取值无关,所以也可以将\\(X\\)的熵记作\\(H(p)\\),即
$$H(p)=-\sum \limits_{i=1}^n p_i \log p_i$$
熵越大,随机变量的不确定性就越大。从定义可以验证
$$0\leq H(p)\leq \log n$$
当随机变量只取2个值时,当取值概率为0/1时,熵为0,此时完全没有不确定性。
条件熵
已知随机变量\\((X,Y)\\)的联合概率分布为:
$$P(X=x_i,Y=y_i)=p_{ij}, i=1,2,...,n;j=1,2,...,m$$
条件熵\\(H(Y|X)\\)表示已知\\(X\\)情况下,\\(Y\\)的分布的不确定性。计算如下:
$$H(Y|X)=\sum \limits_{i=1}^n p_iH(Y|X=x_i)$$
这里,\\(p_i=P(X=x_i),i=1,2,...,n\\)
信息增益
信息增益表示得知了特征\\(X\\)的信息,使得类\\(Y\\)的信息不确定性减小的程度。也叫作互信息(mutual information),决策树中的信息增益等价于训练集中的类与特征的互信息。
特征\\(A\\)对训练数据集\\(D\\)的信息增益\\(g(D,A)\\),定义为集合\\(D\\)的经验熵\\(H(D)\\)与特征\\(A\\)给定条件下\\(D\\)的经验条件熵\\(H(D|A)\\)之差,即
$$g(D,A)=H(D)−H(D|A)$$
决策树学习应用信息增益准则选择特征。信息增益大的特征具有更强的分类能力。
根据信息增益准则的特征选择方法是:对训练数据集(或子集)\\(D\\),计算其每个特征的信息增益,并比较他们的大小,选择信息增益最大的特征。
算法 (信息增益的算法)
输入:训练数据集\\(D\\)和特征\\(A\\);
输出:特征\\(A\\)对训练数据集\\(D\\)的信息增益\\(g(D,A)\\)。
(1) 计算数据集\\(D\\)的经验熵\\(H(D)\\)
$$H(D)=-\sum \limits_{k=1}^K \frac{ | C_k |}{ | D |}\log_2 \frac{ | C_k |}{ | D |}$$
(2) 计算特征\\(A\\)对数据集\\(D\\)的经验条件熵\\(H(D|A)\\)
$$H(D|A)=\sum \limits_{i=1}^n \frac{ | D_i |}{ | D |}H(D_i)=-\sum \limits_{i=1}^n \frac{ | D_i |}{ | D |} \sum \limits_{k=1}^K \frac{ | D_{ik} |}{ | D_i |} \log_2 \frac{ | D_{ik} |}{ | D_i |}$$
(3) 计算信息增益
$$g(D,A)=H(D)-H(D|A)$$
实现信息增益的python代码:
def calc_ent(x): """ calculate shanno ent of x """ x_value_list = set([x[i] for i in range(x.shape[0])]) ent = 0.0 for x_value in x_value_list: p = float(x[x == x_value].shape[0]) / x.shape[0] logp = np.log2(p) ent -= p * logp return ent def calc_condition_ent(x, y): """ calculate ent H(y|x) """ # calc ent(y|x) x_value_list = set([x[i] for i in range(x.shape[0])]) ent = 0.0 for x_value in x_value_list: sub_y = y[x == x_value] temp_ent = calc_ent(sub_y) ent += (float(sub_y.shape[0]) / y.shape[0]) * temp_ent return ent def calc_ent_grap(x,y): """ calculate ent grap """ base_ent = calc_ent(y) condition_ent = calc_condition_ent(x, y) ent_grap = base_ent - condition_ent return ent_grap
信息增益比
以信息增益作为划分训练数据集的特征,存在偏向于选择取值较多的特征的问题。使用信息增益比(information gain ratio)可以对这一问题进行校正。这是特征选择的另一准则。
特征\\(A\\)对训练数据集\\(D\\)的信息增益比\\(g_R(D,A)\\)定义为其信息增益\\(g(D,A)\\)与训练数据集\\(D\\)关于特征\\(A\\)的值的熵\\(H_A(D)\\)之比,即
$$g_R(D,A)=\frac{g(D,A)} {H_A(D)}$$
其中,\\(H_A(D)=-\sum \limits_{i=1}^n \frac{ | D_i |}{ | D |}\log_2 \frac{ | D_i |}{ | D |}\\)
决策树的生成
ID3算法
ID3算法(interative dichotomiser 3)的核心是在决策树各个结点上应用信息增益准则选择特征,递归地构建决策树。具体方法是:从根结点(root node)开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征,由该特征的不同取值建立子结点;再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。ID3相当于用极大似然法进行概率模型的选择。
ID3算法只有树的生成,所以该算法生成的树容易产生过拟合。
算法 (ID3算法)
输入:训练数据集\\(D\\),特征集\\(A\\),阈值\\(\varepsilon\\);
输出:决策树\\(T\\) 。
(1) 如果\\(D\\)中的所有实例属于同一类\\(C_{k}\\) ,则置\\(T\\)为单结点树,并将\\(C_{k} \\)作为该结点的类,返回\\(T\\);
(2) 如果\\(A=\phi\\),则置\\(T\\)为单节点树,并将\\(D\\)中实例数最大的类\\(C_{k}\\)作为该结点的类,返回\\(T\\);
(3) 否则,按\\(g(D,A)=H(D)-H(D|A)\\)计算\\(A\\)中个特征对\\(D\\)的信息增益比,选择信息增益比最大的特征\\(A_{g}\\) ;
(4) 如果\\(A_{g}\\)的信息增益比小于阈值\\(\varepsilon\\),则置\\(T\\)为单结点树,并将\\(D\\)中实例数最大的类\\(C_{k}\\)作为该结点的类,返回\\(T\\);
(5) 否则,对\\(A_{g}\\)的每一可能值\\(a_{i}\\),依\\(A_{g} = a_{i}\\)将\\(D\\)分割为子集若干非空\\(D_{i}\\),将\\(D_{i}\\)中实例树最大的类作为标记,构建子结点,由结点及其子结点构成树\\(T\\)返回\\(T\\);
(6) 对结点\\(i\\),以\\(D_{i}\\)为训练集,以\\(A - \{A_{g} \}\\)为特征集,递归地调用步(1)~步(5),得到子树\\(T_{i}\\),返回\\(T_{i}\\) .
例子 :对下表训练数据,利用ID3算法建立决策树。
下面给出python代码(绘图代码不在建立决策树之内):
import math def majorityCnt(classList): """ 返回出现次数最多的分类名称 :param classList: 类列表 :return: 出现次数最多的类名称 """ classCount = {} # 这是一个字典 for vote in classList: if vote not in classCount.keys(): classCount[vote] = 0 classCount[vote] += 1 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0] def chooseBestFeatureToSplitByID3(dataSet): """ 选择最好的数据集划分方式 :param dataSet: :return: """ numFeatures = len(dataSet[0]) - 1 # 最后一列是分类 baseEntropy = calcShannonEnt(dataSet) bestInfoGain = 0.0 bestFeature = - 1 for i in range(numFeatures): # 遍历所有维度特征 infoGain = calcInformationGain(dataSet, baseEntropy, i) if (infoGain > bestInfoGain): # 选择最大的信息增益 bestInfoGain = infoGain bestFeature = i return bestFeature # 返回最佳特征对应的维度 def createTree(dataSet, labels, chooseBestFeatureToSplitFunc=chooseBestFeatureToSplitByID3): """ 创建决策树 :param dataSet:数据集 :param labels:数据集每一维的名称 :return:决策树 """ classList = [example[-1] for example in dataSet] # 类别列表 if classList.count(classList[0]) == len(classList): return classList[0] # 当类别完全相同则停止继续划分 if len(dataSet[0]) == 1: # 当只有一个特征的时候,遍历完所有实例返回出现次数最多的类别 return majorityCnt(classList) bestFeat = chooseBestFeatureToSplitFunc(dataSet) bestFeatLabel = labels[bestFeat] myTree = {bestFeatLabel: {}} del (labels[bestFeat]) featValues = [example[bestFeat] for example in dataSet] uniqueVals = set(featValues) for value in uniqueVals: subLabels = labels[:] # 复制操作 myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) return myTree def createDataSet(): """ 创建数据集 :return: """ dataSet = [[u'青年', u'否', u'否', u'一般', u'拒绝'], [u'青年', u'否', u'否', u'好', u'拒绝'], [u'青年', u'是', u'否', u'好', u'同意'], [u'青年', u'是', u'是', u'一般', u'同意'], [u'青年', u'否', u'否', u'一般', u'拒绝'], [u'中年', u'否', u'否', u'一般', u'拒绝'], [u'中年', u'否', u'否', u'好', u'拒绝'], [u'中年', u'是', u'是', u'好', u'同意'], [u'中年', u'否', u'是', u'非常好', u'同意'], [u'中年', u'否', u'是', u'非常好', u'同意'], [u'老年', u'否', u'是', u'非常好', u'同意'], [u'老年', u'否', u'是', u'好', u'同意'], [u'老年', u'是', u'否', u'好', u'同意'], [u'老年', u'是', u'否', u'非常好', u'同意'], [u'老年', u'否', u'否', u'一般', u'拒绝'], ] labels = [u'年龄', u'有工作', u'有房子', u'信贷情况'] # 返回数据集和每个维度的名称 return dataSet, labels def splitDataSet(dataSet, axis, value): """ 按照给定特征划分数据集 :param dataSet: 待划分的数据集 :param axis: 划分数据集的特征的维度 :param value: 特征的值 :return: 符合该特征的所有实例(并且自动移除掉这维特征) """ retDataSet = [] for featVec in dataSet: if featVec[axis] == value: reducedFeatVec = featVec[:axis] # 删掉这一维特征 reducedFeatVec.extend(featVec[axis + 1:]) retDataSet.append(reducedFeatVec) return retDataSet def calcShannonEnt(dataSet): """ 计算训练数据集中的Y随机变量的香农熵 :param dataSet: :return: """ numEntries = len(dataSet) # 实例的个数 labelCounts = {} for featVec in dataSet: # 遍历每个实例,统计标签的频次 currentLabel = featVec[-1] if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 shannonEnt = 0.0 for key in labelCounts: prob = float(labelCounts[key]) / numEntries shannonEnt -= prob * math.log(prob, 2) # log base 2 return shannonEnt def calcConditionalEntropy(dataSet, i, featList, uniqueVals): ''' 计算X_i给定的条件下,Y的条件熵 :param dataSet:数据集 :param i:维度i :param featList: 数据集特征列表 :param uniqueVals: 数据集特征集合 :return:条件熵 ''' ce = 0.0 for value in uniqueVals: subDataSet = splitDataSet(dataSet, i, value) prob = len(subDataSet) / float(len(dataSet)) # 极大似然估计概率 ce += prob * calcShannonEnt(subDataSet) # ∑pH(Y|X=xi) 条件熵的计算 return ce def calcInformationGain(dataSet, baseEntropy, i): """ 计算信息增益 :param dataSet:数据集 :param baseEntropy:数据集中Y的信息熵 :param i: 特征维度i :return: 特征i对数据集的信息增益g(dataSet|X_i) """ featList = [example[i] for example in dataSet] # 第i维特征列表 uniqueVals = set(featList) # 转换成集合 newEntropy = calcConditionalEntropy(dataSet, i, featList, uniqueVals) infoGain = baseEntropy - newEntropy # 信息增益,就是熵的减少,也就是不确定性的减少 return infoGain def calcInformationGainRate(dataSet, baseEntropy, i): """ 计算信息增益比 :param dataSet:数据集 :param baseEntropy:数据集中Y的信息熵 :param i: 特征维度i :return: 特征i对数据集的信息增益g(dataSet|X_i) """ return calcInformationGain(dataSet, baseEntropy, i) / baseEntropy # 决策树的构建 myDat, labels = createDataSet() myTree = createTree(myDat, labels)
# 绘制决策树 import matplotlib.pyplot as plt # 定义文本框和箭头格式 decisionNode = dict(boxstyle="round4", color='#3366FF') #定义判断结点形态 leafNode = dict(boxstyle="circle", color='#FF6633') #定义叶结点形态 arrow_args = dict(arrowstyle="<-", color='g') #定义箭头 #绘制带箭头的注释 def plotNode(nodeTxt, centerPt, parentPt, nodeType): createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction', va="center", ha="center", bbox=nodeType, arrowprops=arrow_args) #计算叶结点数 def getNumLeafs(myTree): numLeafs = 0 firstStr = list(myTree.keys())[0] secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': numLeafs += getNumLeafs(secondDict[key]) else: numLeafs += 1 return numLeafs #计算树的层数 def getTreeDepth(myTree): maxDepth = 0 firstStr = list(myTree.keys())[0] secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': thisDepth = 1 + getTreeDepth(secondDict[key]) else: thisDepth = 1 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth #在父子结点间填充文本信息 def plotMidText(cntrPt, parentPt, txtString): xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0] yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1] createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30) def plotTree(myTree, parentPt, nodeTxt): numLeafs = getNumLeafs(myTree) depth = getTreeDepth(myTree) firstStr = list(myTree.keys())[0] cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff) plotMidText(cntrPt, parentPt, nodeTxt) #在父子结点间填充文本信息 plotNode(firstStr, cntrPt, parentPt, decisionNode) #绘制带箭头的注释 secondDict = myTree[firstStr] plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': plotTree(secondDict[key], cntrPt, str(key)) else: plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD def createPlot(inTree): fig = plt.figure(1, facecolor='white') fig.clf() axprops = dict(xticks=[], yticks=[]) createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) plotTree.totalW = float(getNumLeafs(inTree)) plotTree.totalD = float(getTreeDepth(inTree)) plotTree.xOff = - 0.5 / plotTree.totalW; plotTree.yOff = 1.0; plotTree(inTree, (0.5, 1.0), '') plt.show() createPlot(myTree)
我们应该可以得到如下差不多的图:
C4.5的生成算法
C4.5算法与ID3算法相似,C4.5算法对ID3算法进行了改进。C4.5在生成的过程中,用信息增益比来选择特征。
算法 (C4.5的生成算法):
输入:训练数据集\\(D\\),特征集\\(A\\),阈值\\(\varepsilon \\)
输出:决策树\\(T\\)
(1) 如果\\(D\\)中的所有实例属于同一类\\(C_{k}\\) ,则置\\(T\\)为单结点树,并将\\(C_{k} \\)作为该结点的类,返回\\(T\\);
(2) 如果\\(A=\phi\\),则置\\(T\\)为单节点树,并将\\(D\\)中实例数最大的类\\(C_{k}\\)作为该结点的类,返回\\(T\\);
(3) 否则,按\\(g_{R}(D,A) = \frac{g(D/A)}{H_{A}(D)} \\)计算\\(A\\)中个特征对\\(D\\)的信息增益比,选择信息增益比最大的特征\\(A_{g}\\) ;
(4) 如果\\(A_{g}\\)的信息增益比小于阈值\\(\varepsilon\\),则置\\(T\\)为单结点树,并将\\(D\\)中实例数最大的类\\(C_{k}\\)作为该结点的类,返回\\(T\\);
(5) 否则,对\\(A_{g}\\)的每一可能值\\(a_{i}\\),依\\(A_{g} = a_{i}\\)将\\(D\\)分割为子集若干非空\\(D_{i}\\),将\\(D_{i}\\)中实例树最大的类作为标记,构建子结点,由结点及其子结点构成树\\(T\\)返回\\(T\\);
(6) 对结点\\(i\\),以\\(D_{i}\\)为训练集,以\\(A - \{A_{g} \}\\)为特征集,递归地调用步(1)~步(5),得到子树\\(T_{i}\\),返回\\(T_{i}\\) .
实现的python代码(省略与之前重复的代码):
def chooseBestFeatureToSplitByC45(dataSet): """ 选择最好的数据集划分方式 :param dataSet: :return: """ numFeatures = len(dataSet[0]) – 1 # 最后一列是分类 baseEntropy = calcShannonEnt(dataSet) bestInfoGainRate = 0.0 bestFeature = –1 for i in range(numFeatures): # 遍历所有维度特征 infoGainRate = calcInformationGainRate(dataSet, baseEntropy, i) if (infoGainRate > bestInfoGainRate): # 选择最大的信息增益 bestInfoGainRate = infoGainRate bestFeature = i return bestFeature # 返回最佳特征对应的维度
决策树的剪枝
决策树很容易发生过拟合,过拟合的原因在于学习的时候过多地考虑如何提高对训练数据的正确分类,从而构建出过于复杂的决策树。解决这个问题的办法就是简化已生成的决策树,也就是剪枝。
决策树的剪枝往往通过极小化决策树整体的损失函数或代价函数来实现。
决策树生成:考虑更好的拟合训练集数据 —— 学习局部的模型
剪枝:通过优化损失函数还考虑了减小模型复杂度 —— 学习整体的模型
设树T的叶节点个数为\\( |T|\\),每个叶节点即为沿从root的某条路径条件下的一类。\\(t\\)是树\\(T\\)的叶节点,该节点有\\(N_t\\)个样本点,其中属于各个分类的点为\\(N_{tk}\\)个。
该叶节点的经验熵为:
$$H_t(T)=-\sum \limits_{k=1}^K \frac{ | N_{tk} |}{ | N_t |}\log_2 \frac{ | N_{tk} |}{ | N_t |}$$
则决策树学习的损失函数可以定义为:
$$C_{\alpha}(T)=\sum \limits_{t=1}^{ |T |} N_tH_t(T) + \alpha |T|$$
记右端第一项为
$$C(T)=\sum \limits_{t=1}^{ |T |} N_tH_t(T)=-\sum \limits_{t=1}^{ |T |} \sum \limits_{k=1}^{K} N_{tk} \log \frac{N_{tk}}{N_t}$$
有\\(C_{\alpha}(T)=C(T) + \alpha |T|\\)
第一项反映对训练集的拟合程度,第二项反映模型复杂度。等价于正则化的极大似然估计。
L1范数是指向量中各个元素绝对值之和,也叫“稀疏规则算子”(Lasso regularization)。
L2范数是指向量各元素的平方和然后求平方根。
算法 (树的剪枝算法)
输入:生成的树\\(T\\),参数\\(α\\)
输出:子树\\(T_α\\)
(1) 计算每个节点的经验熵。
(2) 递归地从叶节点向上收缩。
设有一组叶节点回缩前后的整体树分别为\\(T_B\\),\\(T_A\\),对应的损失函数如果是:
$$C_{\alpha}(T_A)\leq C_{\alpha}(T_B)$$
剪枝后损失函数更小,则说明应该剪枝,将父结点变为新的叶节点。
(3) 返回(2)直至不能继续为止。得到损失函数最小的子树\\(T_{\alpha}\\)。
注意(1)我们计算的是所有节点的经验熵,虽然我们考虑叶节点比较,但因为不断剪枝时,每个节点都可能变为叶节点。所以计算全部存起来。
注意:每次考虑两个树的损失函数的查,计算可以在局部进行,所以剪枝算法可以由一种动态规划的算法实现。
CART算法
分类与回归树(classification and regression tree, CART),即可用于分类,也可用于回归。由三步组成:特征选择,生成树,剪枝。
CART树假设决策树为二叉树,每个结点为2分支,“是”与“否”。
CART生成
对回归树:平方误差最小化
对分类树:基尼指数-Gini index
回归树的生成
一个回归树对应特征空间的一个划分,每个划分单元上输出一个值。假设已将输入空间划分成\\(M\\)个单元\\(R_1,R_2...,R_M\\),对应输出值为\\(c_1,c_2...,c_M\\),那么,回归树模型表示为:
$$f(x)=\sum \limits_{m=1}^{M} c_mI(x\in R_m)$$
当输入空间的划分确定时,可以用平方误差\\(\sum \limits_{x_i\in R_m} (y_i-f(x_i))^2\\)表示回归树对训练集\\(D\\)的预测误差
每个单元上的均值为\\(\hat{c}_m= ave(y_i|x_i \in R_m)\\)
用启发式的方法对空间进行划分,选择切分变量和切分值:特征的第\\(j\\)个变量,以及其取值\\(s\\),将空间划分为两个子空间:
$$R_1(j,s)= \{x|x^{(j)} \leq s \} 和 R_2(j,s)= \{x|x^(j)>s \}$$
然后我们求解这个划分下的最小值:
$$\min \limits_{j,s} [ \min \limits_{c_1} \sum \limits_{x_i\in R_1(j,s)} (y_i-c_1)^2+\min \limits_{c_2} (y_i-c_2)^2 ]$$
这样,我们可以遍历\\(j\\)和\\(s\\),对每一组情况下,算出[ ]中的最小值。在所有\\(j\\),\\(s\\)组合情况下找出一个最小值。此时的\\(j\\)和\\(s\\)就是我们需要的。第一次划分后,对两个子区域迭代这样做,就可以将空间不断细化。
算法 (最小二乘回归树生成算法)
输入:训练数据集\\(D\\)
输出:回归树\\(f(x)\\)
(1) 选择最优切分变量\\(j\\)和切分点\\(s\\)。求解:
$$\min \limits_{j,s} [ \min \limits_{c_1} \sum \limits_{x_i\in R_1(j,s)} (y_i-c_1)^2+\min \limits_{c_2} (y_i-c_2)^2 ]$$
遍历\\(j\\)和\\(s\\),对某个\\(j\\)扫描\\(s\\),使得上式最小
(2) 用选好的\\((j, s)\\)划分区域,并决定各分区的输出值:
$$R_1(j,s)= \{x|x^{(j)} \leq s \}和 R_2(j,s)= \{x|x^{(j)}>s \}$$
$$\hat{c_m}=\frac{1}{N_m} \sum \limits_{x_i\in R_1(j,s)} y_i$$
$$x \in R_m,m=1,2$$
(3) 继续对两个子区域调用步骤(1),(2),直到满足停止的条件
(4) 将输入空间划分为\\(M\\)个区域\\(R_1,R_2,...,R_M\\),生成决策树:
$$f(x)=\sum \limits_{m=1}^{M} \hat{c_m} I(x\in R_m)$$
分类树的生成
对分类问题,随机变量在每个类上都有概率。以数据集中各类个数比上总数,极大似然估计,得到离散的概率分布。
基尼系数:
$$Gini(x)=\sum \limits_{k=1}^{K} p_k(1-p_k)=1-\sum \limits_{k=1}^{K}p_k^2$$
对于给定的样本集合\\(D\\),基尼指数为
$$Gini(x)=1-\sum \limits_{k=1}^{K} ( \frac{ | C_k |}{ | D |} )^2$$
\\(C_k\\)是\\(D\\)中第\\(k\\)类的个数,\\(K\\)是类别总个数。
若样本集合\\(D\\)根据特征\\(A\\)是否取某一可能值\\(a\\)被划分为\\(D_1\\),\\(D_2\\),则在特征\\(A\\)的条件下,集合\\(D\\)的基尼指数为
$$Gini(D,A)=\frac{ |D_1 |}{ |D |}Gini(D_1)+\frac{ |D_2 |}{ |D |}Gini(D_2)$$
算法 (CART生成算法)
输入:训练数据集\\(D\\),停止计算的条件
输出:CART决策树
根据训练数据集,从根结点开始,递归地对每个结点进行一下操作,构建二叉决策树:
(1)设结点的训练数据集为\\(D\\),计算现有特征对该数据集的基尼指数。此时,对每一个特征\\(A\\),对其可能取的每个值\\(a\\),根据样本点对\\(A=a\\)的测试是“是”或“否”将\\(D\\)分割成\\(D_1\\)和\\(D_2\\)两部分
(2)在所有可能的特征\\(A\\)以及它们所有可能的切分点\\(a\\)中,选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点,依最优特征与最优切分点,从现结点生成两个子结点,将训练数据集依特征分配到两个子结点中
(3)对两个子结点递归地调用(1),(2),直至满足停止条件
(4)生成CART决策树
算法停止的条件是结点中的样本个数小于预定阈值,或样本集的基尼指数小于预定阈值(样本基本属于同一类),或者没有更多特征。
CART剪枝
CART剪枝算法从“完全生长”的决策树的底端剪去一些子树,使决策树变小(模型变简单),从而能够对未知数据有更准确的预测。CART剪枝算法由两步组成:首先,从生成算法产生的决策树\\(T_0\\)底端开始不断剪枝,直到\\(T_0\\)的根结点,形成一个子树序列\\( \{T_0,T_1,⋯,T_n \}\\);然后,通过交叉验证法在独立的验证数据集上对子树序列进行测试,从中选择最优子树。
剪枝,形成一个子树序列
在剪枝过程中,计算子树的损失函数:
$$C_{\alpha}(T)=C(T) + \alpha |T|$$
可以用递归的方法对树进行剪枝,将\\(a\\)从小增大,\\(\alpha_0<\alpha_1<...<\alpha_n<+\infty \\),产生一系列的区间\\([\alpha_i,\alpha_{i+1}),i =0,1,...,n\\);剪枝得到的子树序列对应着区间\\(\alpha \in [\alpha_i,\alpha_{i+1}),i =0,1,...,n\\)的最优子树序列\\( \{T_0, T_1, ... , T_n \}\\),序列中的子树是嵌套的。
对\\(T_0\\)中每一内部结点\\(t\\),计算
$$g(t)=\frac{C(t)-C(T_t)} { |T_t |-1}$$
表示剪枝后整体损失函数减少的程度,在\\(T_0\\)中剪去\\(g(t)\\)最小的\\(T_t\\),将得到的子树作为\\(T_1\\),同时将最小的\\(g(t)\\)设为\\(\alpha_1\\),\\(T_1\\)为区间\\([\alpha_1,\alpha_2)\\)的最优子树。如此剪枝下去,直至得到根结点。在这一过程中,不断地增加\\(\alpha\\)的值,产生新的区间。
在剪枝得到的子树序列\\(T_0,T_1, ... , T_n\\) 中通过交叉验证选取最优子树\\(T_a\\)
具体地,利用独立的验证数据集,测试子树序列\\(T_0, T_1, ... , T_n\\)中各棵子树的平方误差或基尼指数。平方误差或基尼指数最小的决策树被认为是最优的决策树。在子树序列中,每棵子树\\(T_0, T_1, ... , T_n\\)都对应于一个参数\\(a_0, a_1, ... , a_n\\)。所以,当最优子树\\(T_k\\)确定时,对应的\\(a_k\\)也确定了,即得到最优决策树\\(T_a\\)。
算法 (CART剪枝算法)
输入:CART算法生成的决策树\\(T_0\\)
输出:最优决策树\\(T_a\\)
(1) 设\\(k=0\\),\\(T=T_0\\)
(2) 设\\(\alpha=+\infty\\)
(3) 自下而上地对各内部的点\\(t\\)计算\\(C(T_t)\\),\\( |T_t |\\)以及
$$g(t)=\frac{C(t)-C(T_t)} { |T_t |-1}$$
$$\alpha=\min(\alpha,g(t))$$
这里,\\(T_t\\)表示以\\(t\\)为根结点的子树,\\(C(T_t)\\)是对训练数据的预测误差,\\( |T_t |\\)是\\(T_t\\)的叶结点个数
(4) 对\\(g(t)=\alpha\\)的内部结点\\(t\\)进行剪枝,并对叶结点\\(t\\)以多数表决法决定其类,得到树\\(T\\)
(5) 设\\(k=k+1,\alpha_k=\alpha,T_k=T\\)
(6) 如果\\(T_k\\)不是由根结点及两个叶结点构成的树,则回到步骤(3);否则令\\(T_k=T_n\\)
(7) 采取交叉验证法在子树序列\\(T_0,T_1,...,T_n\\)中选取最优子树\\(T_a\\).
小结
(1)分类决策树模型,是表示基于特征对实例进行分类的树的结构。决策树可换成一个if-then规则的集合。也可看做是定义在特征空间划分上的类的条件概率分布。
(2)决策树学习的目的是构建一个与训练集拟合很好,并且复杂度小的决策树。从可能的决策树中直接选取最优决策树是NP完全问题,实际中采用启发式方法学习次优的决策树。
(3)学习算法有ID3,C4.5,CART。学习过程包括:特征选择,生成树,剪枝。特征选择目的在于选择对训练集能够分类的特征。特征选取的准则三种算法分别是信息增益最大,信息增益比最大,基尼系数最小。从根节点开始,递归产生决策树,分别对子树调用过程,不断选取局部最优特征。
(4)由于生成的决策树存在过拟合问题,需要剪枝。从生成的树上剪掉一些叶节点或者叶节点以上的子树,将其父节点或者根节点作为新的叶节点,简化生成的决策树。
参考资料
- Author:Quanfita
- URL:https://quanfita.cn/article%2Fdecision_tree
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!
Relate Posts
